“To see a World in a grain of sand, and a Heaven in a wild flower, Hold Infinity in the palm of your hand, and Eternity in an hour.”
To efficiently search the computational universe, the market needs to be organized for effective information reusablity. Traditionally, the role of information reusability is played by financial intermediaries such as investment banks, brokers or traders. They are the information processing and storage elements of the financial universe. How they are different, at a very high level, is simply that: investment bankers have capital and clients and are able to act as principals in trades; brokers have information and clients and are able to act as agents representing clients in trades; and proprietary traders have capital but no clients and have to find information to process in order to generate profitable trades.
Information has a peculiar property: its use does not result in its consumption. Most goods and services are transformed into waste as a result of being used. But this is not the case with information. Properly reusing information can result in substantial savings. To appreciate the power of information reusability, consider the following “wildcatting” metaphor from the book “Contemporary Financial Intermediation”:
“Think of a very large geographic grid in which each intersection represents a potential oil well. Now suppose there are many oil drilling entrepreneurs, and further suppose that after drilling a dry hole the law requires that the landscape be restored to its initial condition. Thus, there is no way to know if a particular location has been drilled unless there is an operating well at a particular location. If a broker simply collects and disseminates information about the drilling activities of each explorer, the cost of redrilling dry holes can be eliminated. Without the broker, society will bear the unnecessary cost of searching for oil in locations known to be unproductive.”
Go Wild Cats! Massive oil fields discovered in 1911, South Belridge, California. (Image Credit: Edward Burtynsky).
One can see that the larger the grid, the more compelling the need for a broker. For a given grid size, the more complex the object of search (e.g., whose attributes are less easily observable or subject to judgment), the more important the skills and reputation of the broker. An important aspect of brokerage is that it can be performed without processing substantial risks. In other words, brokerage services can be produced risklessly, in principle, and the processing of risk is not central to the production of brokerage services. But this is not the case with trading services built around asset transformation.
So what exactly do traders do? Traders look for mismatch of attributes in assets across the financial universe, and seek to transform them. Common asset attributes include: duration (or term to maturity), divisibility (or unit size), liquidity, credit risk, and numeraire (i.e., which currency). Typically, with respect to assets whose attributes they seek to transform, they can choose to either shorten the duration by holding assets of longer duration than its own liabilities; reduce the unit size by holding assets of larger unit size than its liabilities; enhance liquidity by holding assets that are more illiquid than its liabilities; or reduce credit risk by holding assets that are more likely to default than its liabilities. And by holding assets denominated in a different currency than its liabilities, they can also alter the numeraire of the assets. Traders collect a premium for carrying out asset transformation services in the financial markets, which they then share with investors whom they trade with to become the asset owners.
The case of duration transformation is particularly illustrative. The yield curve is thought to be a “biased predictor” of future spot interest rates owing to a liquidity premium attached to longer duration claims. Typically, borrowers prefer to borrow long-term, and lenders prefer to lend short-term. This is the theory of term structure of interest rates according to Sir John Hicks, a British economist who coined the term “forward interest rates” around 1925 in a London café when considering this matter. When traders are introduced into such a financial world, they would be able to finance the purchase of long-term assets with short-term liabilities, and profit from doing so. In fact, traders would continue to perform this transformation until the liquidity premium is competed down to the marginal cost of intermediating. According to Hicks, if the yield curve were an unbiased predictor of future spot interest rates, there would be no profit in performing duration transformation. Liquidity premium is what keeps the traders in the game.
One can say that the regenerative power of the world’s economy is derived from the redistributive property of trading in the global financial markets. Trading reallocates capital resources to where they are most needed, diversifies or shifts the risks, unifies markets, and improves liquidity. Using a biological metaphor, we can consider trading as the “lifeblood” of an organism, providing it with strength and energy by circulating nutrients to the right places in the body, shifts and distributes weights across the body, and make different body parts work together to improve overall mobility. Without financial trading, the world’s economy would fragment into a thousand uncoordinated pools of activities, operate at a greatly reduced level of efficiency, and yield a poor economic utility for all of its market participants. In short, a rather unhappy lump of organic matter, totally stressed out and unable to move at all.
So we seek to identify and occupy a sustainable trading niche that lies somewhere along the spectrum between the extremes of arbitrage (i.e., riskless, transitory, but requires high speed) and speculation of future asset prices (i.e., high risk, need to wait longer duration, and requires massive memory). Arbitrages of the non-statistical types are rare, and we cannot rely upon them to build a steady trading business. On the other hand, speculations abound, but they carry high risks and we won’t last very long in the trading business without a reliable means of hedging risks. What we are looking for would be classified as “risk-controlled arbitrage” or “limited risk speculation”. Therefore, we should learn to design trades that can hedge out risks, and find trade combinations that work nicely without tying up capital beyond the duration required for executing the trades. A potential candidate niche that might work for us is arbitrage trading based on speculated statistical models. We don’t necessarily have the fastest speed, but we are adequately provisioned when it comes to organizing storage memory in the cloud. We can work with lots of bits.
We have a hunch that information reusability is a key piece of the puzzle when it comes to assembling the parts of the MVP. We will be sure to examine this aspect of information a little closer, from both the cross-sectional reusability aspect (i.e., the same information can be reused across instruments or markets) as well as from the intertemporal aspect (i.e., reused through time). We know that redundant searches could be expensive, from both computational and budgetary considerations, and a well-designed MVP should provide architectural support for this type of savings. It’s a giant grid to explore, after all, and we do not have a lot of computational resources (neither bits nor time) to waste.
"It from Bit": A Holographic Universe for Computation. (Image Credit: Ars Technica).
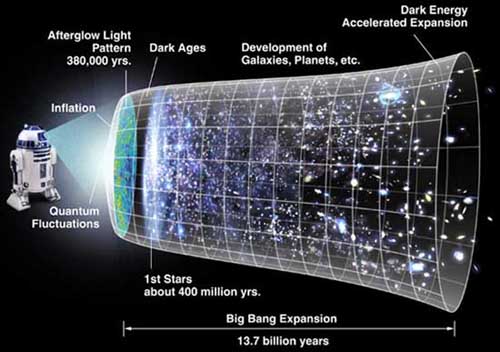
It is natural to ask: how might the universe be finite in computational resources? For instance, how many storage bits are there in the entire universe? Let’s start with the concept of “entropy” which, when considered as information (aka Shannon entropy), is measured in bits. The total quantity of bits is related to the total degrees of freedom of matter and energy. For a given energy in a given volume, there is an upper limit to the density of information, aka the Bekenstein bound, about the whereabouts of all the particles which compose matter in that volume. This suggests that matter itself cannot be subdivided infinitely many times; there has to be some ultimate upper limit as to the number of fundamental particles. The reason is that if a particle were to be subdivided infinitely into sub-particles, then the degrees of freedom of the original particles must be infinite, as the degrees of freedom of a particle are the product of all the degrees of freedom of its sub-particles. This would obviously violate the maximal limit of entropy density, according to the calculations of Jacob Bekenstein.
We can thus consider the fundamental particle as represented by a bit (i.e., “zero” or “one”) of information. What matters for computational purposes is not the spatial extent of the universe, but the number of physical degrees of freedom located in a causally connected region. In the standard cosmological models, the region of the universe to which we have causal access at this time is limited by the finite speed of light and finite age of the universe since the Big Bang. In 2002, Seth Lyold calculated the total number of bits available to us in the universe for computation to be around 10122. This upper bound is not fixed, but grows with time as the horizon expands and encompasses more particles.
Similarly, one might consider upper bounds on computational speed for the universe. In fact, Hans-Joachim Bremermann suggested back in 1962 that there is a maximum information-processing rate, which we now call Bremermann’s limit, for a physical system that has a finite size and energy. In other words, a self-contained system in the material universe has a maximum computational speed. For example, a computing device with the mass of the entire Earth operating at the Bremermann’s limit could perform approximately 1075 computations per second. This is important when designing cryptographic algorithms. We only hope that we’ll never run into Bremermann in computational finance.
“Is she real? Or are we but shadows on Plato’s cave?" C3PO wondered.
The Holographic Principle postulates that the total information content of a region of space cannot exceed one quarter of the area of its encompassing surface (called the "event horizon"). The principle was first proposed by Gerard ‘t Hooft in 1993 and further elaborated by Leonard Susskind. A simple calculation of the size of our universe’s event horizon today, based on the size of the event horizon created by the measured value of dark energy, gives an information bound of 10122 bits, which is the same as found by Lyold using the “particle horizon”. The event horizon also expands with time, and at present is roughly the same radius as the particle horizon. Regardless of which method is used as the basis for the calculation, they agree on an upper bound for the information content of a causal region of the universe.
It was the theoretical physicist John A. Wheeler who first considered “the physical world as made of information, with energy and matter as incidentals.” Could our universe, in all its richness and diversity, really be just a bunch of bits? To some, an ultimate theory of reality must be concerned less with fields or spacetime, but rather with information exchange among physical processes. That sounds like computational finance, e.g., think about how the term structure of interest rates today already encodes all forward interest rates of any duration projecting into the future. It is quite possible our physical universe may be a hologram after all.
“In a universe limited in resources and time — concepts like real numbers, infinitely precise parameter values, differentiable functions, the unitary evolution of a wave function – are a fiction: a useful fiction to be sure, but a fiction nevertheless, and with the potential to mislead. It then follows that the laws of physics, cast as idealized infinitely precise mathematical relationships inhabiting a Platonic heaven, are also a fiction when it comes to applications to the real universe.”
References:
- Greenbaum, Stuart I. and Thakor, Anjan V. (2007). Contemporary Financial Intermediation (Second Edition). Academic Press.
- Davies, P.C.W. (2007, March 6). The Implications of a Cosmological Information Bound for Complexity, Quantum, Information and the Nature of Physical Law. Retrieved from: http://arxiv.org/abs/quant-ph/0703041
- Seth, Lyold (2002). Computational Capacity of the Universe. Physical Review Letters, 88, 237901, 1-17. Retrieved from: http://cds.cern.ch/record/524220/files/0110141.pdf
- Bekenstein, Jacob D. (2003, August). Information in the Holographic Universe — Theoretical results about black holes suggest that the universe could be like a gigantic hologram. Scientific American, 289, pp. 58-65. Retrieved from: http://www.nature.com/scientificamerican/journal/v289/n2/pdf/scientificamerican0803-58.pdf
- Bremermann, Hans J. (1962). Optimization through Evolution and Recombination. In: Self Organizing Systems (Editors: M.C. Yovits, G.T. Jacobi, and G.D. Goldstein), Spartan Books, pp. 93-106.